Uttaedru
In giumitria solida, l' uttaedru hè un puliedru incù ottu facci triangulari. L'uttaedru rigulari hè un di i cinqui solidi platonichi, chì i so facci sò trianguli equilateri. Hà sei vertici è dodici spiculi.
Aria è vulumu
[mudificà | edità a fonte]L'aria di superficia è u vulumu di l'uttaedru rigulari di u quali spiculu hà una lunghezza sò dati da:
U vulumu hè 4 volti quiddu d'un tetraedru rigulari incù spiculi di lunghezza , mentri l'aria di superficia hè u doppiu (apposta ch'edda hè furmata da 8 trianguli equilateri, quandu u tetraedru inveci n'hà 4)
L'angulu diedrali di l'uttaedru rigulari hè arc cos(-1/3), apprussimativamenti uguali à 109.47122°.
Cuurdinati cartisiani
[mudificà | edità a fonte]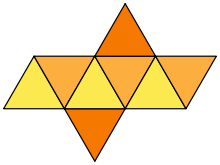
Un uttaedru rigulari in u spaziu euclidea pò essa traslatu di manera à avè u centru in l'urighjina, è dopu à oppurtuni rutazioni è similitudina hà i 6 vertici in
A custruzzioni di Euclide
[mudificà | edità a fonte]

In u libru XIII di i so Elementi, Euclide discrivi u metudu par iscriva un uttaedru rigulari in una sfera di diamitru datu. A custruzzioni discritta da Euclide hè a siguenti:
Sii AB (vedi Fig. 1) u diamitru di a sfera data; si trovi u so puntu mediu D è si tracci un mezuchjerchju di centru D è raghju DA. Si alza a parpindiculari da D, ditarminendu u puntu C nantu à a circumfarenza è infini si cunghjunghjini i punti AC è CB.
Si riplicheghji listessa custruzzioni annantu à i trè piani passendu par AB incù un angulu diedru di 90°, 180° è 270° rispettu à u pianu iniziali (Fig. 2). Si tracciani infini i cunghjunghjenti frà i punti CE, EF, FG è GC.
Hè chjaru ch'è i vertici A, C, E, F è G si trovani annantu à i mezicircumfarenzi custruiti nantu à u diamitru AB, è dunqua si trovani tutti nantu à a superficia di a sfera di listessu diamitru. Par custruzzioni i spiculi chì partini da i vertici A è B sò uguali trà eddi; ma ancu i spiculi CE, EF, FG è GC ani listessa lunghezza: infatti tutti i spiculi di l'uttaedru sò dinò l'iputenusa d'un triangulu rittangulu di u quali i cateti sò raghji di a sfera.
Par ciò chì riguarda u rapportu frà diamitru di a sfera spiculu di l'uttaedru iscrittu, par via di u tiurema di Pitagora u quatratu custruitu nantu à u spiculu hè doppiu di u quatratu custruitu nantu à u raghju di a sfera; par via di cunsiquenza u quatratu custruitu nantu à u diamitru hè doppiu di u quatratu custruitu nantu à u spiculu.
Puliedru duali
[mudificà | edità a fonte]U puliedru duali di l'uttaedru rigulari hè u cubu.
Simmitrii
[mudificà | edità a fonte]L'uttaedru hà 24 simmitrii rutaziunali, veni à dì chì priservani l'uriintazioni di u spaziu, più altri 24 simmitrii chìùn a priservani micca. U gruppu di simmitria di l'uttaedru conta dunqua un tutali di 48 elementi.
U sottugruppu datu da i 24 rutazioni hè isumorfu à u gruppu di i parmutazioni di 4 elementi. Ci hè infatti asattamenti una rutazioni chì rializeghja ogni pussibuli parmutazioni di i 4 coppii di facci opposti.
U gruppu tutali di simmitria hè isumorfu à u pruduttu di incù un gruppu ciclicu incù 2 elementi.
Impavimenti
[mudificà | edità a fonte]

L'uttaedru rigulari ùn inghjinireghja micca da solu un impavimentu di u spaziu, parchì i so anguli diedrali ùn sò micca divisori di 360°. Ni inghjinireghja una parò in cumbinazioni incù u tetraedru, com'è mustratu annantu à a figura.
Da veda dinò
[mudificà | edità a fonte]- Solidu platonicu
- Uttaedru truncatu
- Uttaedru iperbolicu
- Toru (giumitria)
- Giumitria piana
- Angulu rettu
- Catetu
- Mezaretta
- Perimetru
- Sigmentu
- Triangulu isusceli
- Triangulu equilateru
- Tiurema di Pitagora
- Iputenusa
- Tangenti
- Trigunumitria
- Triangulu
Noti
[mudificà | edità a fonte]
Fonti
[mudificà | edità a fonte]'Ss'articulu pruveni in parti o in tutalità da l'articulu currispundenti di a wikipedia in talianu.











