Triangulu equilateru

Triangulu equilateru

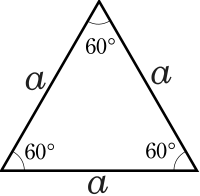
Un triangulu equilateru hè un triangulu incù tutti i lati cungruenti è dunqua hè un poligunu rigulari incù trè lati. L'anguli sò tutti uguali è pari à 60° = ${\frac {\pi }{3}}$rad.

I trianguli equilateri sò trianguli isusceli particulari. Tutti i trianguli equilateri sò simili trà eddi: par carattarizà metricamenti un triangulu equilateru, vali à dì par carattarizà a classa di i trianguli equilateri in u pianu chì si poni uttena l'uni da l'altri par via di traslazioni è rutazioni, servi è basta un parametru estinsivu: tipicamenti s'usa a lunghezza di i so lati.

In i trianguli equilateri, i bisettrici, i mediani, l'altezzi è l'assi si soprapponini di tali manera ch'è listessu puntu ripprisenta l'ortucentru, u baricentru, l'incentru è u circucentru.

U gruppu di i simmetrii di u triangulu equilateru hè custituitu da l'idantità, da i rutazioni intornu à u so centru di 120° è di 240° è da i riflissioni rispettu à i bisettrici di l'anguli. Stu gruppu hè isumorfu à u gruppu simetricu di 3 ughjetti S₃.

Custruzzioni

Custruzzioni di u triangulu equilateru incù riga è cumpassu

Com'è a dimostra Euclide in i so Elementi I, 1 (hè a prima prupusizioni di tutta l'opara), u triangulu equilateru datu u latu AB si pò custruiscia incù riga è cumpassu in 'ssa manera:

• Si poni u cumpassu in A incù l'apartura AB è si traccia una circumfarenza;
• Si poni u cumpassu in B incù l'apartura BA è si traccia una circumfarenza;
• U puntu d'incontru di i circumfarenzi C hè u terzu puntu circatu;
• Uniscendu A, B è C s'otteni un triangulu equilateru.

A dimustrazioni hè simplicia: essendu, par difinizioni, tutti i punti di a circumfarenza equidistanti da u centru, u sigmentu AB hè cungruenti à AC, è AB hè cungruenti à BC. Ma tandu par a prubità transitiva di a cungruenza, AB = AC = BC è u triangulu hè equilateru.

Formuli

Rifirendu si incù $l$ à u latu di u triangulu, incù $2P$ u perimetru, incù $A$ l'aria, incù $b$ a basa è incù $h$ l'altezza s'hà:

Perimetru

$2P=l\cdot 3$

$l={\frac {2P}{3}}$

Aria

$A={\frac {b\cdot h}{2}}={\frac {l^{2}}{4}}\cdot {\sqrt {3}}$

$h={\frac {A\cdot 2}{b}}$

$b={\frac {A\cdot 2}{h}}$

Appiigazioni di u Tiurema di Pitagora

$h={\sqrt {l^{2}-\left({\frac {l}{2}}\right)^{2}}}={\sqrt {l^{2}-{\frac {l^{2}}{4}}}}={\sqrt {\frac {4l^{2}-l^{2}}{4}}}={\sqrt {\frac {3l^{2}}{4}}}={\frac {{\sqrt {l^{2}}}\cdot {\sqrt {3}}}{\sqrt {4}}}={\frac {{l}\cdot {\sqrt {3}}}{2}}={\frac {l}{2}}{\sqrt {3}}$

$l={\frac {2h}{\sqrt {3}}}$

Circumfarenza inscritta è circuscritta

U centru giumetricu di u triangulu hè u centru di i circumfarenzi iscritta è circuscritta à u triangulu equilateru

U raghju di a circumfarenza circuscritta hè $R={\frac {\sqrt {3}}{3}}l$

da u quali $l=R{\sqrt {3}}$

U raghju di a circumfarenza inscritta hè $r={\frac {\sqrt {3}}{6}}l$

da u quali $R=2\cdot r$

Aria (nota R) $A={\frac {3\cdot R^{2}}{4}}\cdot {\sqrt {3}}$

Da veda dinò

• Criterii di cungruenza di i trianguli
• Triangulu
• Triangulu isusceli
• Triangulu scalenu
• Toru (giumitria)
• Giumitria piana
• Angulu rettu
• Catetu
• Mezaretta
• Perimetru
• Sigmentu
• Tiurema di Pitagora
• Iputenusa
• Tangenti
• Trigunumitria
• Uttaedru

Fonti

'Ss'articulu pruveni in parti o in tutalità da l'articulu currispundenti di a wikipedia in talianu.