Cungittura di Goldbach
In matematica, a cungittura di Goldbach (o congettura di Golbach) hè un di i più vechji prublemi irrisuluti in a tiuria di i numari. Afferma ch'è ogni numaru paru più maiò ch'è 2 pò essa scrittu com'è a somma di dui numari primi (chì poni essa ancu uguali).
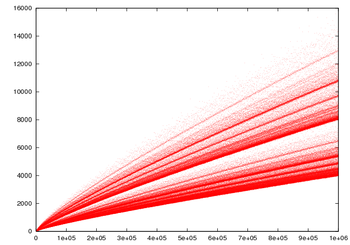
Par asempiu :
- 4 = 2 + 2
- 6 = 3 + 3
- 8 = 3 + 5
- 10 = 3 + 7 = 5 + 5
- 12 = 5 + 7
- 14 = 3 + 11 = 7 + 7
- etc.
Urighjini
[mudificà | edità a fonte]In 1742, u matematicu prussianu Christian Goldbach scrissi una lettara à Eulero ind'eddu li pruposi a siguenti cungittura:
- Ogni numaru intreiu più maiori ch'è 5 pò essa scrittu com'è somma di trè numari primi.
Eulero, intarissendu si à u prublemu, risposi rifurmulendu u prublemu in a siguenti virsioni equivalenti:
- Ogni numaru paru più maiori ch'è 2 pò essa scrittu com'è somma di dui numari primi.
A virsioni di Eulero hè a forma in a quali a cungittura hè furmulata à i ghjorna d'oghji ed hè calchì volta dinuminata cungittura forti di Goldbach. A cungittura debuli di Goldbach, chì hè implicata da a cungittura forti, asserisci ch'è tutti i numari dispari più maiori ch'è 7 poni essa scritti com'è somma di trè primi dispari.
Risultati
[mudificà | edità a fonte]A cungittura di Goldbach hà attrattu l'attinzioni di molti tiurichi di i numari. A maiò parti di i matematichi riteni ch'è a cungittura hè vera, basendu si par u più annantu à cunsidarazioni statistichi è prubabilistichi ottinuti incù u tiurema di i numari primi.
In u 1923 Hardy è Littlewood ani dimustratu ch'è s'è l'iputesi di Riemann generalizata hè vera, tandu a cungittura debuli di Goldbach hè vera par tutti l'intrei dispari abbastanza grandi. In u 1937, Ivan Vinogradov cacceti l'assunzioni di l'iputesa di Riemann generalizata, mustrendu ch'è ogni numaru disparu hè somma di trè primi. Inoltri, basendu si nantu à l'idei di Vinogradov, Chudakov,[1] van der Corput,[2] è Estermann[3] ani dimustratu ch'è guasi tutti i numari pari poni essa scritti com'è somma di dui primi, veni à dì ch'è a frazzioni di i numari chì poni essa scritti in 'ssu modu tendi à 1. In 1975, Hugh Montgomery è Robert Vaughan ani datu una virsioni più pricisa di stu risultatu mustrendu ch'è u numaru d'intrei pari più minori ch'è N chì ùn sò micca ripprisintevuli com'è somma di dui primi hè più minori ch'è par dui custanti .
Parechji altri risultati parziali sò stati dimustrati in u corsu di l'anni. In u 1939 L.G. Schnirelmann pruvò ch'è ogni numaru paru n ≥ 4 pò essa scrittu com'è somma di à u più 20 numari primi.Stu numaru hè statu abbassatu [4] dopu da numarosi matematichi, in particulari Olivier Ramaré in u 1995, hà dimustratu ch'è ogni numaru paru n ≥ 4 si pò scriva com'è somma di à u più 6 numari primi. Si ussirvò dinò ch'è a cungittura debuli di Goldbach implicheghja u listessu risultatu, ma incù soli 4 numari primi.
In 1951, Linnik hà dimustratu ch'eddu esisti un intreiu k tali ch'è ogni numaru paru abbastanza grandi si pò scriva com'è somma di dui primi è à u più k putenzi di dui. In u 2002 Roger Heath-Brown è Jan-Christoph Schlage-Puchta ani dimustratu ch'è k = 13 hè sufficienti[5] è in u 2003 Pintz è Ruzsa ani migliuratu stu risultatu mustrendu ch'eddu si pò piglià k = 8.[6]
Un antru risultatu impurtanti hè quiddu ottinutu da Chen Jingrun chì in u 1966 hà dimustratu ch'è ogni numaru paru abbastanza grandi pò essa scrittu com'è somma o di dui primi, o d'un prima è un mezu primu (u pruduttu di dui primi - par asempiu, 100 = 23 + 7·11).[7]
Infini, in u corsu di l'anni ci sò stati parechji risultati par abbassà a limita minziunata sopra aldilà di a quali a cungittura debuli di Goldbach hè dimustrata. Trà quiddi, ci hè a dimustrazioni di Deshouillers, Effinger, te Riele è Zinoviev ch'è l'iputesa di Riemann generalizata implicheghja a cungittura debuli di Goldbach.[8] In u 2013 Harald Helfgott hà annunciatu d'avè dimustratu 'ssu risultatu senza l'assunzioni di l'iputesa di Riemann, risulvendu tutalamenti dunqua a cungittura debuli di Goldbach.[9][10][11][12]
Citazioni in l'arti
[mudificà | edità a fonte]- In 2000, à u scopu di fà a riclama par u libru Ziu Petros è a cungittura di Goldbach di Apostolos Doxiadis, l'editori britannicu Tony Faber uffrì un premiu di 1 000 000 di dullari par una dimustrazioni di a cungittura. U premiu saria statu assignatu solu par dimustrazioni inviati par a publicazioni prima d'aprili 2002, ma ùn fù mai riclamatu.
- A cungittura di Goldbach hè citata in u filmu A Bestia incù un miliardu di schieni, virsioni cinematugrafica di a seria animata Futurama, in una scena in a quali u professor Farnsworth è u so rivali-cullega prof. Wernstrom affermani d'avè truvatu "un'antra dimustrazioni elementari" di a cungittura di Goldbach.
- Hè citata in u libru U tiurema di u pappagallu di Denis Guedj.
- Hè citata in u libru Parchì eiu credu in Quiddu chì hà fattu u mondu. Trà fedi è scenza di Antonio Zichichi.
- Hè citata in u filmu spagnolu La habitación de Fermat.
- Hè citata in u prima racontu (Milioni di trilioni) di I banchetti di i veduvi neri d'Isaac Asimov
Noti
[mudificà | edità a fonte]- ↑ Nikolai G. Chudakov, О проблеме Гольдбаха [On the Goldbach problem] in «Doklady Akademii Nauk SSSR», 1937, pp. 335–338.
- ↑ J. G. Van der Corput, Sur u hypothèse de Goldbach in «Proc. Akad. Wet. Amsterdam», 1938, pp. 76–80.
- ↑ T. Estermann, On Goldbach's problem: proof that almost à l even pusitivi integers are sums of two primes in «Proc. London Math. Soc.», 1938, pp. 307–314. DOI:10.1112/plms/s2-44.4.307.
- ↑ Citazioni nicissaria.
- ↑ D. R. Heath-Brown; J. C. Puchta, Integers represented as à sum of primes and powers of two in «Asian Journal of Mathematics», (3), 2002, pp. 535–565. arXiv:math.NT/0201299.
- ↑ J. Pintz; I. Z. Ruzsa, On Linnik's approximation to Goldbach's problem, I in «Acta Arithmetica», (2), 2003, pp. 169–194. DOI:10.4064/aa109-2-6.
- ↑ J. R. Chen, On the representation of à larger even integer as the sum of à primi and the product of at most two primes. Sci. Sinica 16 (1973), 157--176.
- ↑ Deshouillers, Effinger, Te Riele and Zinoviev, A cumpletti Vinogradov 3-primes theorem under the Riemann hypothesis in «Electronic Research Announcements of the American Mathematical Society», (15), 1997, pp. 99–104. DOI:10.1090/S1079-6762-97-00031-0.
- ↑ H.A. Helfgott, Major arcs for Goldbach's theorem, 2013.
- ↑ H.A. Helfgott, Minor arcs for Goldbach's problem, 2012.
- ↑ Primi numbers: the 271 year old puzzle resolved - Truth Is Cool
- ↑ [http://www.newscientist.com/article/dn23535-proof-that- an-infiniti-number-of-primes-are-paired.html Proof that an infiniti number of primes are paired - physics-math - 14 May 2013 - New Scientist]
Bibliugrafia
[mudificà | edità a fonte]- Ziu Petros è a cungittura di Goldbach (1992), di Apostolos Doxiadis, Bompiani (ISBN 88-452-4861-5)
- L'ostinazioni d'un matematicu, vali à dì comu mora trè volti par a cungittura di Goldbach (2005), di Didier Nordon, Sironi Editori (ISBN 88-518-0047-2)
Da veda dinò
[mudificà | edità a fonte]Fonti
[mudificà | edità a fonte]'Ss'articulu pruveni in parti o in tutalità da l'articulu currispundenti di a wikipedia in talianu.




